La Platine Beaglebone, Tutoriels, Trucs et Astuces.
Linear Feedback Shift Register with VHDL.
1- LFSR 16-bit Fibonacci VHDL Code
Let's have a look at this linear feedback shift register, an example choosen from a Wikipedia article.
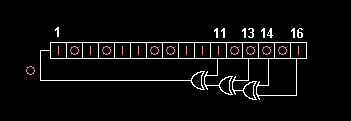
The feedback tap numbers in white correspond to a primitive polynomial so the register cycles through the maximum number
of 65535 (2^16 - 1) states excluding the all 0's state. The state ACE1 shown (hex) will be followed by 5670 (hex).
(Image and text above courtesy of Wikipedia)
The following code is an implementation of this 16-bit Fibonacci LFSR:
library ieee; use ieee.std_logic_1164.all; entity lfsr_n is generic(constant N: integer := 16); port ( clk :in std_logic; reset :in std_logic; lfsr_out :out std_logic_vector (N-1 downto 0) ); end entity; architecture behavioral of lfsr_n is signal lfsr_tmp :std_logic_vector (N-1 downto 0) := (0=>'1', others=>'0'); constant polynome :std_logic_vector (0 to N-1) := "1011010000000000"; begin process (clk, reset) variable feedback :std_logic; begin feedback := lfsr_tmp(0); for i in 1 to N-1 loop feedback := feedback xor ( lfsr_tmp(i) and polynome(i) ); end loop; if (reset = '1') then lfsr_tmp <= (0=>'1', others=>'0'); elsif (rising_edge(clk)) then lfsr_tmp <= feedback & lfsr_tmp(N-1 downto 1); end if; end process; lfsr_out <= lfsr_tmp; end architecture;
The initial value of the LFSR, called the seed, is initialized to 000...01 in the code but it could be change to any N-bit number.
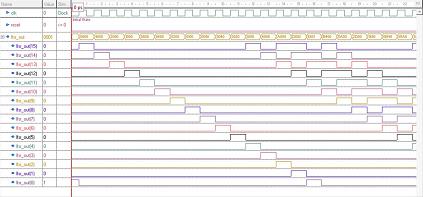
You will get these waveforms if you launch a simulation using
Active HDL software (Clock stimulator: 1Ghz / Time: 50us).
The taps used for this 16-bit Fibonacci LFSR are [16,14,13,11] so it's why the polynome constant in the VHDL file above is
coded as 1011010000000000 in binary. You may obtain a list of all possible taps visiting this website.

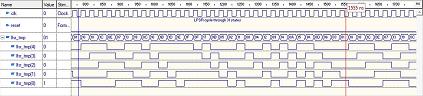
If you want to try for example to simulate a 5-bit Fibonacci LFSR, just change the N constant to 5 in the code above and
the polynome constant to 11101 corresponding to the taps [5,4,3,1].
You will be able to verify on the waveform below that the LFSR cycles through 31 (2^5 - 1) different states before it repeats.
Don't forget that you may obtain a list of all possible taps visiting this website.
2- LFSR 16-bit Galois VHDL Code
Let's have a look at this linear feedback shift register, an example choosen from a Wikipedia article.

The register numbers in white correspond to the same primitive polynomial as the Fibonacci example but are counted in reverse
to the shifting direction. This register also cycles through the maximal number of 65535 states excluding the all 0's state. The state ACE1 (hex) shown will be followed by E270 (hex).
(Image and text above courtesy of Wikipedia)
The following code is an implementation of this 16-bit Galois LFSR:
library ieee;
use ieee.std_logic_1164.all;
entity galois_n is
generic(constant N: integer := 16);
port (
clk :in std_logic;
reset :in std_logic;
lfsr_out :out std_logic_vector (N-1 downto 0)
);
end entity;
architecture behavioral of galois_n is
signal lfsr_tmp :std_logic_vector (N-1 downto 0):= (0=>'1',others=>'0');
constant polynome :std_logic_vector (N-1 downto 0):= "1011010000000000";
begin
process (clk, reset)
variable lsb :std_logic;
variable ext_inbit :std_logic_vector (N-1 downto 0) ;
begin
lsb := lfsr_tmp(0);
for i in 0 to N-1 loop
ext_inbit(i):= lsb;
end loop;
if (reset = '1') then
lfsr_tmp <= (0=>'1', others=>'0');
elsif (rising_edge(clk)) then
lfsr_tmp <= ( '0' & lfsr_tmp(N-1 downto 1) ) xor ( ext_inbit and polynome );
end if;
end process;
lfsr_out <= lfsr_tmp;
end architecture;
You will get this waveform if you launch a simulation using
Active HDL software (Clock stimulator: 1Ghz / Time: 50us).
The taps used for this 16-bit Galois LFSR are [16,14,13,11] so it's why the polynome constant in the VHDL file above is
coded as 1011010000000000 in binary.
You may obtain a list of all possible taps visiting this website.
